Generating Random Numbers On Decimal Machines
Porting a phrase generator from a binary (2's complement) machine to a decimal (0-9) machine started the following -
The randomizer was considered too slow and not optimized for decimal machines -
Table of Contents, most recent at top
- from Michael Albaugh Dec 20, 2019 2:57 pm
- from Michael Albaugh Dec 13, 2019 9:20 am
- from Robert Garner Dec 12, 2019 7:36 pm
- from Michael Albaugh Dec 05, 2019 10:21 am
- from Robert Garner Dec 04, 2019 10:12 pm
- from Ronald Mak/SJSU Dec 02, 2019 11:11 pm
- from Robert Garner Dec 02, 2019 11:02 pm
- from Michael Albaugh Dec 02, 2019 4:53 pm
- from Ronald Mak Dec 02, 2019 11:56 am
- from Robert Garner December 1, 2019 at 10:32 PM
- A paper by Ron Mak Decimal Random Number Generation - updated Nov 20, 2019
- A paper on Random Number Generators for Decimal Machines - last reference dated 1962
- An e-mail from Ron Mak dated Nov 29, 2019
- from Mike Albaugh Nov 11, 2019
- - from Robert Garner Nov 11, 2019
from Michael Albaugh - Dec 20, 2019 2:57 pm
attached file FMakRand-f.txt
|
An update on my experiments, including a surprise.
... Context: > A Fortran version of MakRand() would also have multiply and divide by ten in place > of the moves, in the rotates: (typed in a hurry, please excuse typos) > > IMSDS = IR1/1000 ISOLATE R1 MSDS > ILSDS = IR1-(IMSDS*1000) ISOLATE R1 LSDS > IR1 = (ILSDS*1000)+IMSDS COMBINE TO COMPLETE ROTATE 3 PLACES RIGHT > IMSDS = IR2/100000 ISOLATE R2 MSDS > ILSDS = IR2-(IMSDS*100000) ISOLATE R2 LSDS > IR2 = (ILSDS*100000)+IMSDS COMBINE TO COMPLETE ROTATE 5 PLACES RIGHT > > Two divides, four multiplies. I probably missed some optimization, but still, I feel the > major issue is "You can't say that in 1401 Fortran" (or not concisely)So I decided to actually implement a small test program. As predicted above, I badly muffed the hasty transcription, but the code attached runs, and produces the same first 20 numbers as the Autocoder version. Concentrating on my third question: > 3) Can MakRand() retain its efficiency edge implemented in 1401 FORTRAN. > (I suspect not, given that there are four multiplies and two divides inherent in the > Fortran version.) So I looked at the generated code snippet of first rotate, which I annotated before findingout that the "indexing" was actually a type flag (A-bit or B-bit but not AB -> Integer): C ISOLATE R1 MSDS 7 IMSDS = IR1/1000 4745: B 700 CALL Interp 4749: DCW @6PW#6MW/GUF@ : IMSDS+X2 # IR1+X2 / CONST1000+X1 4760: DCW @|@ RETURN? C ISOLATE R1 LSDS 8 ILSDS = IR1-(IMSDS*1000) 4761: B 700 CALL Interp 4765: DCW @6OW#6PW*GUFN&6MW@ : ILSDS+X2 # IMSDS+X, * CONST1000+X1 N & IR1 4781: DCW @|@ Return C COMBINE TO COMPLETE ROTATE 3 PLACES RIGHT 9 IR1 = (ILSDS*10000)&IMSDS 4782: B 700 CALL Interp 4786: DCW @6MW#6OW*GVA&6PW@ : IR1+X2 # ILSDS+X2 * CONST10K+X1 & IMSDS+X2 4801: DCW @|@ Return C DITTO FOR R2, 5 PLACES 10 IMSDS = IR2/100000 4802: B 700 The thing that leapt out at me was that integer arithmetic is also interpreted, although we (or at least I) had assumed only FP was. The operand type is encoded in the zone bits of the tens digit of addresses (I went down a rabbit hole trying to make sense of what appeared to be +X2) So that first string, after a bit of massage because I forgot to set FORTRAN character set, and to split it up as the interpreter would see it: 6PW integer at 4676, which the listing says is IMSDS = assignment 6MW int @ 4646, IR1 / GUF int constant 1000 | (record mark) end of expression I did not really expect the compiler to recognize mul/div by powers of ten and convert to Moves, but then I did not expect integer arithmetic to be interpreted either. Anyway, this confirms that my highest priority should be figuring out how to define user functions and patch the library to include them. If I can figure that out, it would be cool to add MakRand to our library. -Mike |
from Michael Albaugh - Dec 13, 2019 9:20 am
|
> On Dec 12, 2019, at 8:52 PM, Robert Garner > > Mike, > >> If I understand what you are saying, we would be discarding the vast majority of values in the use-case of "pick a number from >= 0 and <= 11". >> Might swamp the benefit of avoiding "slow" multiplies and divides. :-) > > The execution time does go up by a factor 1/.12 = 8.3, I may have misunderstood your proposal. When you said "Assuming Ron?s random number generator is uniform [0..99], then all you need to do is discard any value not in the (also uniformly distributed) range of [0..11]" to mean "generate values in [0..99] and discard all those in [12..99]. In fact, that seems to approximate your calculation above. > but Ron?s algorithm (rotation of 7-digits numbers by 3 and 5 digits) is still more than 8.3x faster than > your traditional algorithm that includes 2 multiplies and 2 divisions using 5-digit values. :) All but one multiplication are artifacts of implementing in FORTRAN, and in the general case that multiplication is in the code "surrounding" the PRNG: 206 ISEED = (ISEED * 13849) + 23861 Above multiply is inherent in a Linear Congruential PRNG. Various algorithmic hacks to speed up multiplies by a constant may have reduced effectiveness in a version tailored to the machine radix (2 for most machines, 10 for 1401) because the "A" and "C" values should be mutually prime to the modulus, which is a power of the machine radix. We just have to take one for the team. C TAKE MODULO 65536 TO MIMIC ORIGINAL BINARY ITOP = ISEED/65536 ISEED = ISEED - (ITOP * 65536) Divide and multiply are caused by using a binary radix, and by 1401 Fortran lacking a "modulus". With A, C, and M chosen for a decimal machine, they can be replaced by a "move" (or shift and mask), but only in assembly language. C CONVERT TO FLOAT AND MAP 0..65536. to 0..1.0 RNDNO = ISEED RNDNO = RNDNO/65535. Above divide is to scale to match the library routine's output from zero to (1-epsilon). INDEX=FACT(J2) + (FACT(J2+1)-FACT(J2)) *RNDNO + 1. Above multiply is in the "user" code. If we are interested in a generic PRNG, some equivalent will be in the resulting program. A Fortran version of MakRand() would also have multiply and divide by ten in place of the moves, in the rotates: (typed in a hurry, please excuse typos) IMSDS = IR1/1000 ISOLATE R1 MSDS ILSDS = IR1-(IMSDS*1000) ISOLATE R1 LSDS IR1 = (ILSDS*1000)+IMSDS COMBINE TO COMPLETE ROTATE 3 PLACES RIGHT IMSDS = IR2/100000 ISOLATE R2 MSDS ILSDS = IR2-(IMSDS*100000) ISOLATE R2 LSDS IR2 = (ILSDS*100000)+IMSDS COMBINE TO COMPLETE ROTATE 5 PLACES RIGHT Two divides, four multiplies. I probably missed some optimization, but still, I feel the major issue is "You can't say that in 1401 Fortran" (or not concisely) >> Further, if the selected index selects a blank "word?, we "Roll the dice again" This only happens for the >> first category (subject), where there are only 4 actual words among 12 potential. > > This should be just fine ? the 4 resulting values from Ron?s generator should still be uniformly distributed. The original 2-digit values may well be uniformly distributed, but the "catchment basin" for some of [0..4] will not, because the sampling is still biased. I think there are three questions and we are mixing them up:
-Mike |
from Robert Garner - Dec 12, 2019 7:36 pm
|
Ron,
I've finally tried out the basic frequency test for randomness ? that each digit occurs with the same uniform likelihood ? against your 7-digit and 2-digit rotation-based random numbers, including when the values are limited to the range (0..1). If my program is correct, your generator seems to pass with high marks!! :)))
This first test uses the "chi-square" statistic (well-known-to-you as you?ve been teaching a statistics class this semester! :)
The random number generator testing literature recommends a p-value of > 0.01.
The good news is that, if my Python program is correct, your generator passed with p-values well above 0.01 (dependent on the seed values chosen).
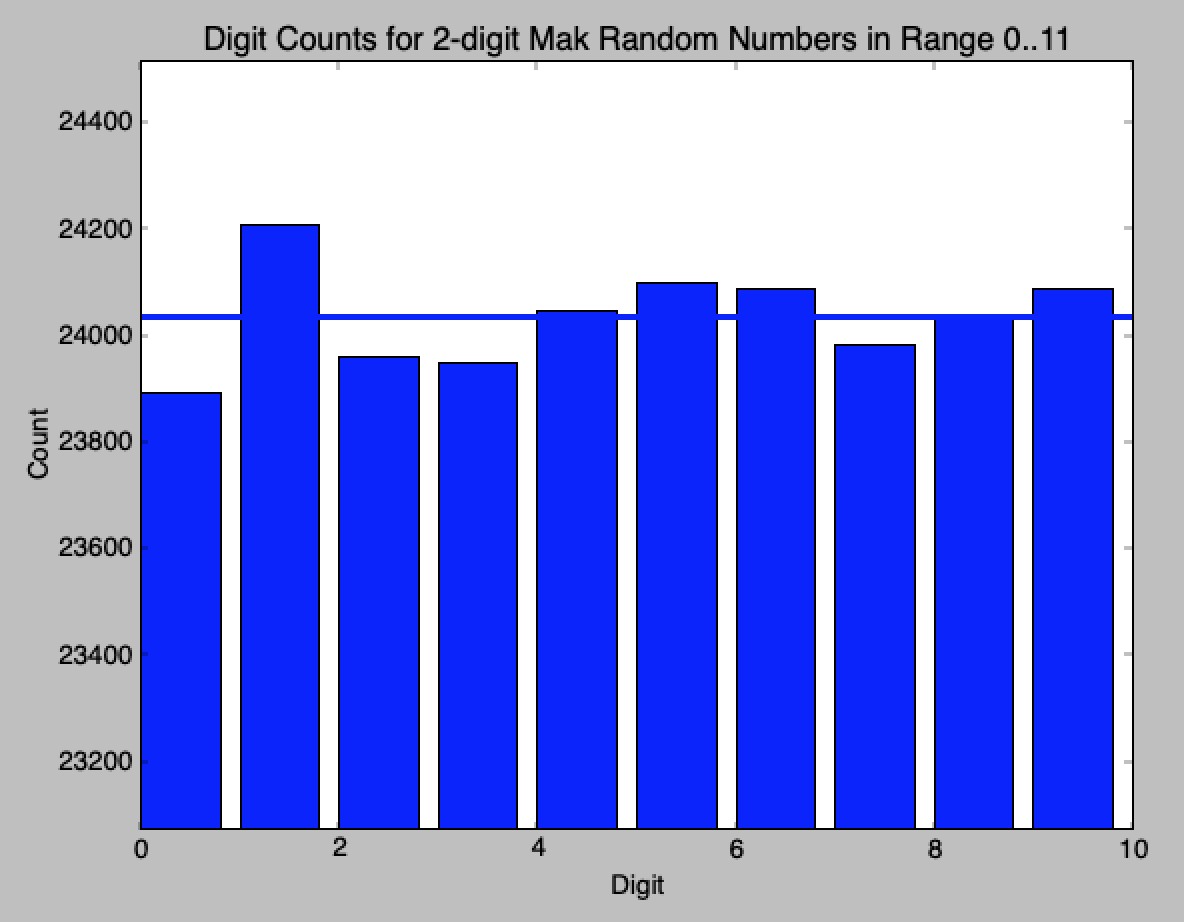
chi-square p-value 7-digit 5.33 0.80 2-digit 5.46 0.79 2-digit (0..11) 3.11 0.96 10-digit RAND 13.3 0.15So your rotation generator appears better than the 1948 RAND table based on this basic test. :)) Here are the metrics with your original seed values of r1 = 1234567 and r2 = 8901234, slightly worse, but still OK: chi-square p-value 7-digit 11.5 0.243 2-digit 16.2 0.062 2-digit (0..11) 4.90 0.96 10-digit RAND 13.3 0.843Here are charts of the digit counts (frequencies) using my seeds:
seeds = 9728491 7929039 Expected count per digit = 700000 Digit counts for 7-digit Mak random numbers = [700721, 700441, 700199, 699981, 701126, 699929, 699720, 699034, 699297, 699552] Chi-square & p-value = (5.3338142857142854, 0.80429228229309513) Expected count per digit = 200000 Digit counts for 2-digit Mak random numbers = [200065, 200444, 199449, 200262, 200188, 199955, 200377, 199431, 199914, 199915] Chi-square & p-value = (5.4574300000000004, 0.7927506241585508) Expected count per digit = 24032 Digit counts for 2-digit Mak random numbers in range (0..11) = [23891, 24204, 23958, 23946, 24045, 24096, 24083, 23979, 24035, 24085] Chi-square & p-value = (3.1137224224165916, 0.95961489985879811) Mean of Mak 2-digit random values = 49.5 Standard Deviation of Mak 2-digit random values= 28.5788383249 Standard Deviation of normally distributed sample averages = 2.85788383249And the Python program: MakNormG_rbg4.py Next up to try are the ?poker? test (pairs, threes, etc), runs test, how soon it repeats, etc., ?
Maybe this is a good time to give this assignment to one of your students??
Cheers, - Robert |
from Michael Albaugh - Dec 05, 2019 10:21 am
While we are chasing questions above my pay grade, I have a (possibly silly) question of my own. We started with LINE GENERATOR and its use of a (FORTRAN library?) PRNG. While the many parts of that program seem designed to be parameterized, the actual instance we have always uses 12 for (max) the number of words in each category, so it scales a float in the range [0,1) to be an integer index 1..12. If the PRNG generates only two decimal digits, can it be mapped evenly into 12 buckets? (Aside: although the following line INDEX=FACT(J2) + (FACT(J2+1)-FACT(J2)) *RNDNO + 1. is an example of possible future parameterization, as written (FACT(J2+1)-FACT(J2)) is always 12) In fact, enumerating all 100 possibilities from the PRNG, we see "preference" for 0,3,6, and 9 (1,4,7,10 if 1-based) with favored numbers appearing 9 times instead of 8. More digits from the PRNG make the preference smaller, but it never goes away (and rounding just favors a slightly different set). So, is there a reason for limiting the precision of the returned value? Would we be better off returning a float as the FORTRAN PRNG does? (The FP interpreter apparently includes a normalize function, so need not be horrible.) --- Further Diversion --- Further, if the selected index selects a blank "word", we "Roll the dice again" This only happens for the first category (subject), where there are only 4 actual words among 12 potential. (Aside 2: I could have hard-coded that line above with explicit 12 and eliminated a F.P. multiply, but have some scruples). I have to wonder if the statistics for successors to a given number are not skewed. If they are, the "catchment" for a given actual word in a sparse set are skewed. Please take these questions as coming from the non-mathematcian that I am. I am just curious. And of course mindful of JVN's caution. :-) -Mike |
from Robert Garner - Dec 04, 2019 10:12 pm
> You are having way too much geek-fun with this ...
Indeed! :))
Ron,
I?m thinking you devilishly suggested this exercise in order to distract me from evaluating how random your generator actually is,
since, in the limit, any RV distribution tends to a normal distribution according to the Central Limit Theorem (CLT)! ;~}
In following plots, I?ve included (in green) the implied normal distribution according to the CLT,
where its Standard Deviation (SD) equals the SD of the sample averaged distribution
(yours in this case, averaged ?Mak Random Variables? :)
divided by the square root of the number of sample averages (num_udrv).
In all the following plots, the runs are for 1 million sampled averages (num_ndrv = 1000000).
Note that in my v3 (attached), I float?d the calculation of the average/mean value of the sample.
(In your program, you had truncated it to an integer.)
I?ve also plotted both curves as Probability Density Functions (so area under them = 1.0)
Here?s the plot for num_udrv=1000 (too many RVs averaged):
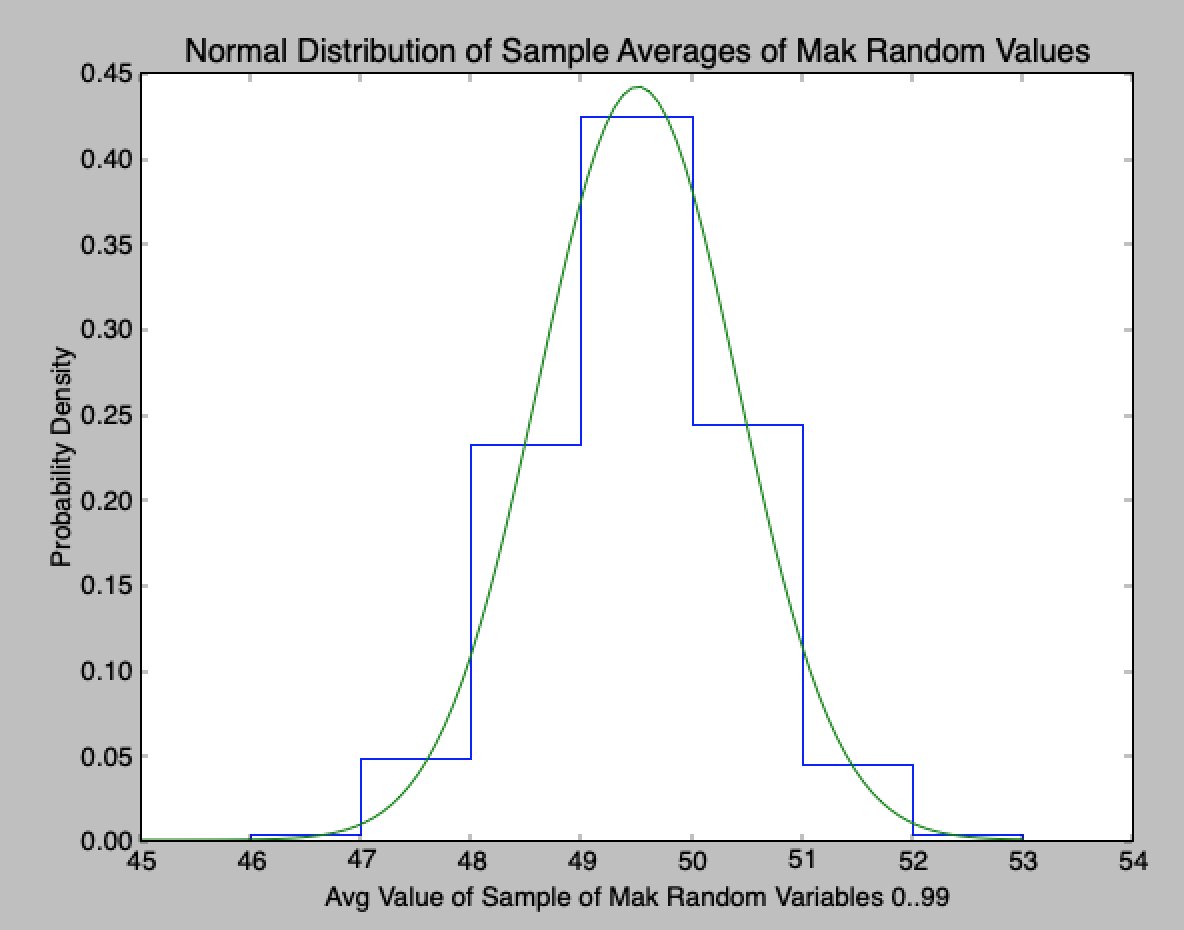
Here?s the plot for num_udrv=100 (better):
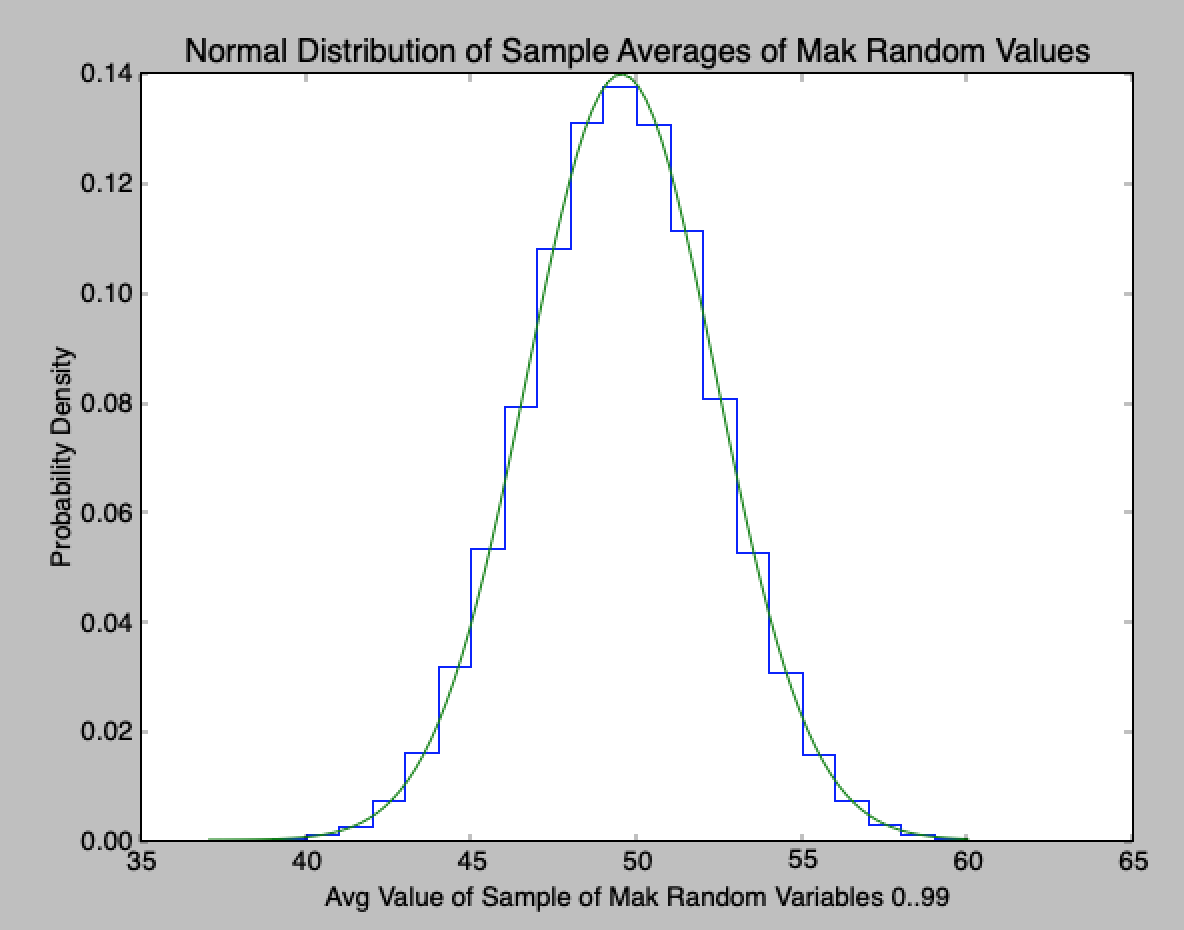
num_udrv=30 (quite good):
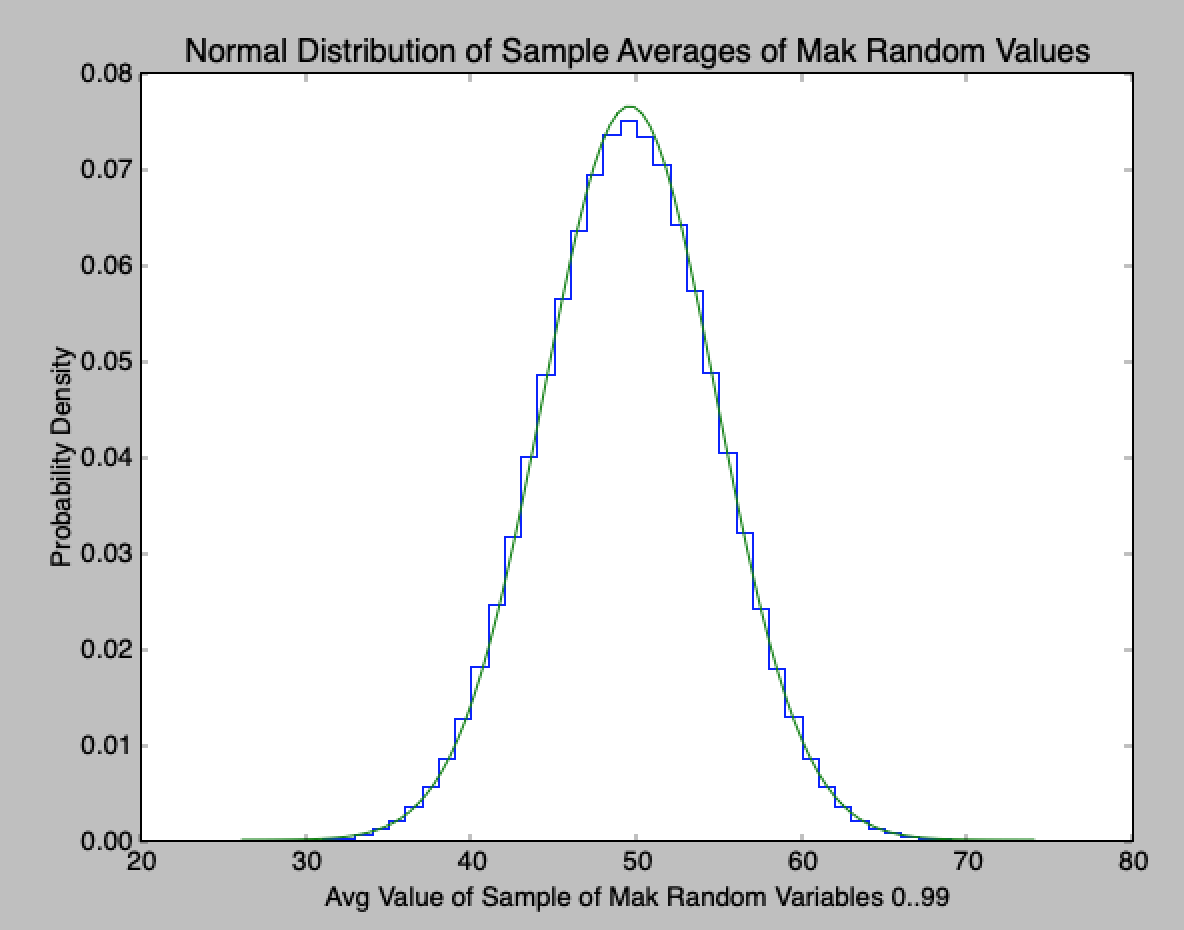
num_udrv=12 (some drooping around the mean):
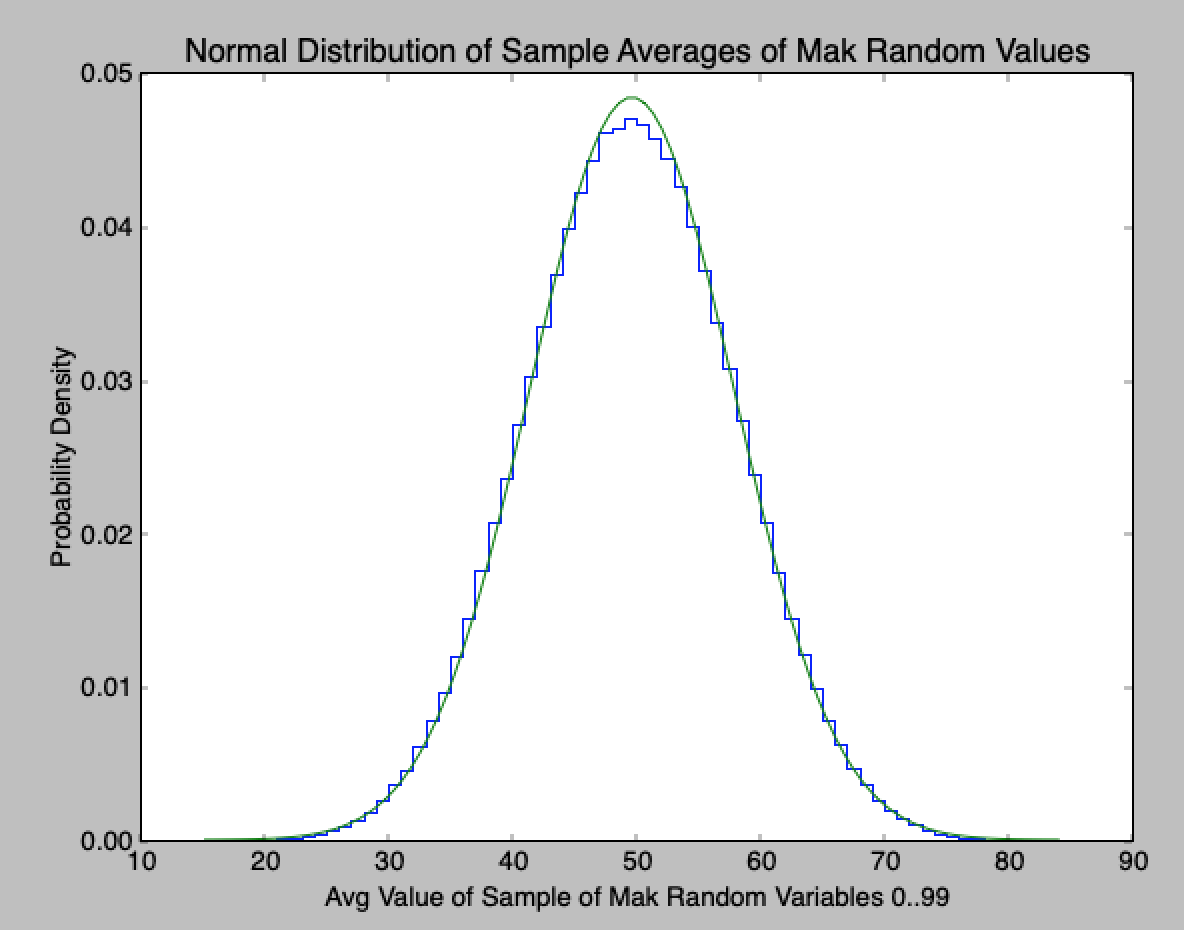
num_udrv=3 (more drooping around the mean):
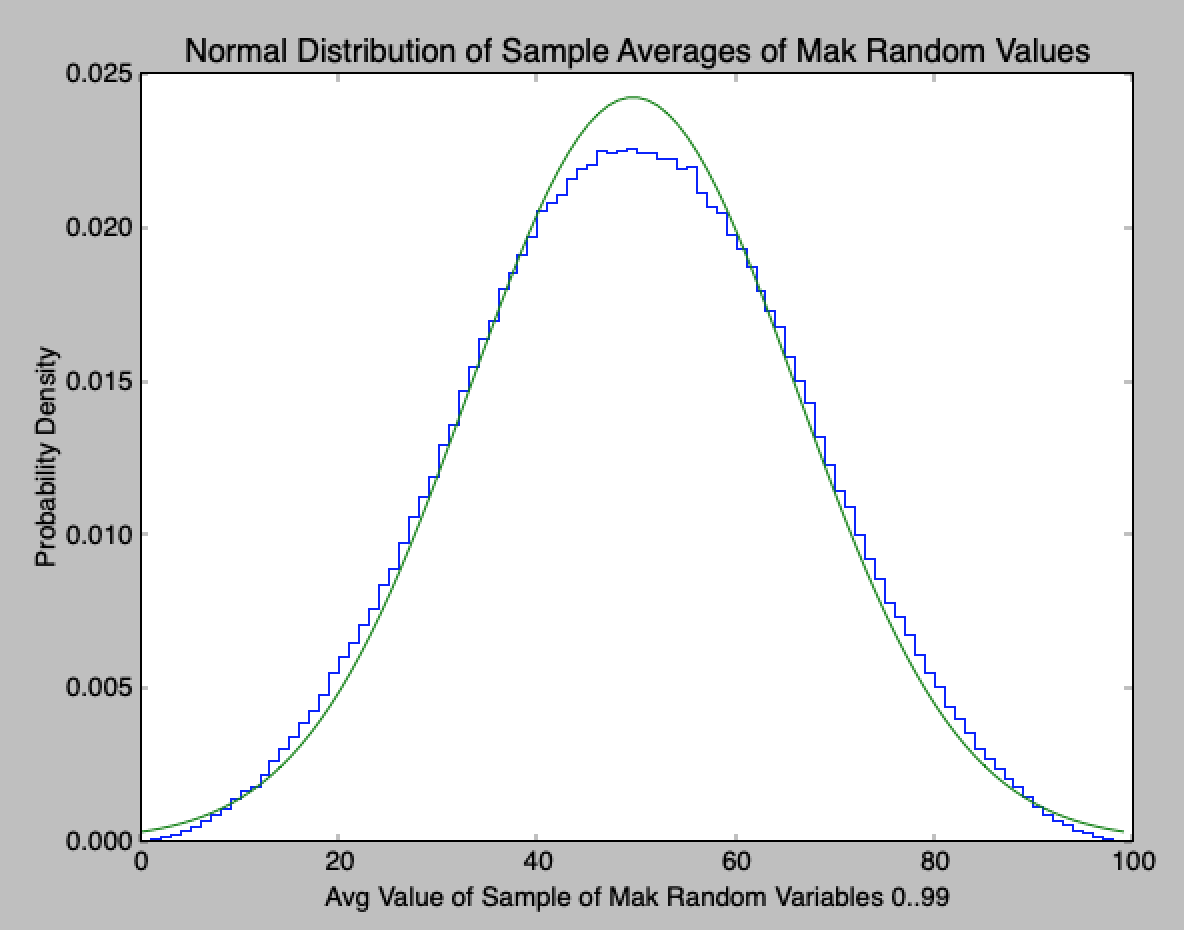
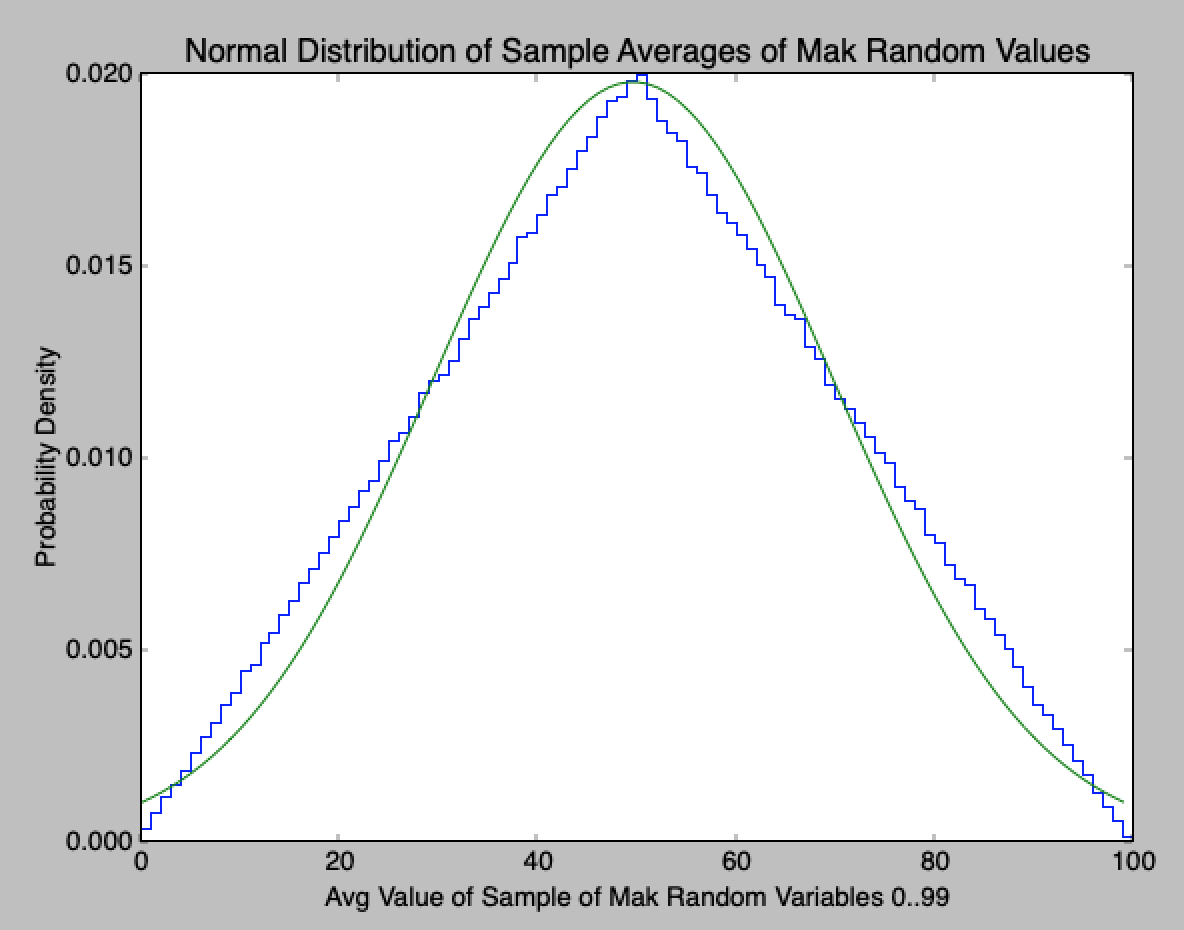
num_udrv=2 (still remarkably close, I wouldn?t have guessed this):
Ok, enough of the CLT, and on to testing how good a RV generator you?ve invented! :)
(First question: How soon does it repeat?
And Sensitivity to seeds? Diehard tests, ..
- Robert
import os, sys
lib_path = os.path.abspath('/Users/rbg/Documents/SimPy')
sys.path.append(lib_path)
import matplotlib.pyplot as plt
import numpy as np
import math as m
from scipy.stats import norm
num_ndrv = 1000000 # number of normally distributed random variables to generate
num_udrv = 100 # number of uniformily distributed random variables to average
# Circular buffer of the last samples_udrv uniformly distributed random values.
buffer = np.array([0]*num_udrv)
x2 = 0
# Running sum of the last 100 uniformly distributed random values.
sum = 0
nrvs = [] # empty list to contain the normal random values
r1 = 1234567 # seed
r2 = 8901234 # seed
# Loop to generate 10,000 normally distributed random values {0..99}
for i in range(num_ndrv + num_udrv - 1):
# Generate the next uniformly distibuted random value urv.
r1 = 10000*(r1%1000) + r1//1000 # rotate right 3 digits
r2 = 100*(r2%100000) + r2//100000 # rotate right 5 digit
s = (r1 + r2)%10000000 # add, and keep the sum to 7 digits
urv = s//100000 # use only the leftmost 2 digits
# Update sum by subtracting the oldest uniform random value
# and adding the latest uniform random value.
sum = sum - buffer[x2] + urv
buffer[x2] = urv # insert urv into the circular buffer
x2 = (x2 + 1) % num_udrv
# After the buffer has filled, start recording the averages.
# Each average is the current sum divided by num_udrv. The averages
# are normally distributed per the Central Limit Theorem.
if i >= (num_udrv-1) : nrvs.append(float(sum//num_udrv))
r1 = r2
r2 = s
# print "The first 20 averaged uniformily distributed random values:", nrvs[0:19]
mean = 0.5 * 99.0
sd_udrv = 99.0 / m.sqrt(12.0)
sd_ndrv = sd_udrv / m.sqrt(float(num_udrv))
print "Mean of Mak Random Values = ", mean
print "Standard Deviation of Mak Random Variables = ", sd_udrv
print "Standard Deviation of Normally Distributed RVs according to CLT = ", sd_ndrv
# plot the resulting, apprxomately normal distribution
numbins = max(nrvs) - min(nrvs) + 1
plt.hist(nrvs, bins=numbins, range=(min(nrvs), max(nrvs)+1), normed=True, histtype='step')
plt.title("Normal Distribution of Sample Averages of Mak Random Values")
plt.xlabel("Avg Value of Sample of Mak Random Variables 0..99")
plt.ylabel("Probability Density")
# plot implied normal distribution curve
x = np.linspace(min(nrvs), max(nrvs), 100)
plt.plot(x, norm.pdf(x, mean, sd_ndrv))
plt.show()
| Don?t go below the sample size of 30, otherwise the Central Limit Theorem no longer applies. |
from Robert Garner Dec 02, 2019 11:02 pm
|
Ron,
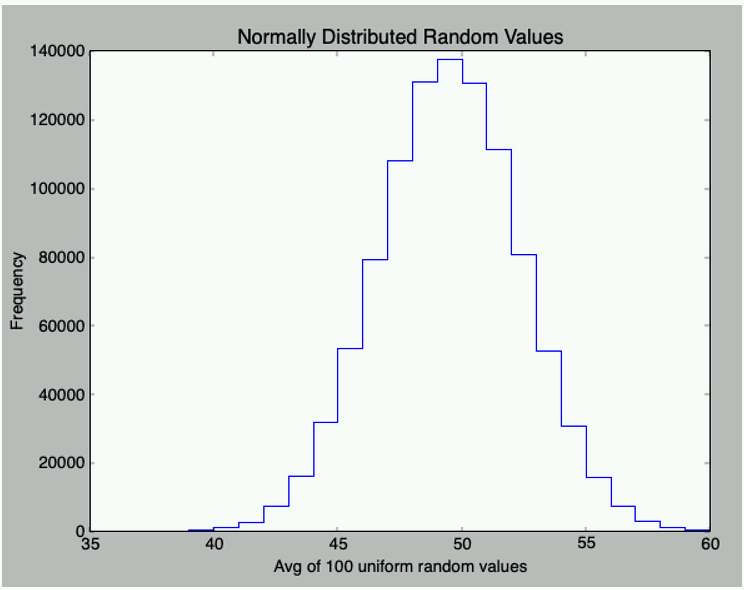
> Generate 1,000,000 random values and you?ll get a much nicer bell curve. Here?s the histogram with 1,000,000 bins, where each bin is average of 100 Mak-Random values:
|
from Michael Albaugh Dec 02, 2019 4:53 pm
|
> On Dec 2, 2019, at 11:56 AM, Ronald Mak/SJSU > > Generate 1,000,000 random values and you?ll get a much nicer bell curve. How long will that take on the 1401? Hmmm. Using my rough memory of instruction timing (this is called "covering my ass about wild errors") I get about 209 clock cycles (92 for instruction fetch, 117 for data) to _generate_ one value (counting the Return, but not the Call), so at 11.5 uSec per clock, that would be 2403.5 uSec per value. So a million values would take 2403.5 seconds roughly 40 minutes. Of course the time taken for the analysis of those values is not included. If someone wants to port Python to the 1401, I'm not gonna stop you, but I'm not holding your beer. :-) Generation code snippet with times (I and D for Instruction and Data cycles):
* PRNG PROPER
ORG 500
MAKRND SBR MRRTN&3 SAVE RETURN ADDRESS
* I 5 D 3
* ROTATE R1 RIGHT BY THREE CHARACTERS.
MCW R1-3,ACC MOVE NUM MSDS TO ACC LSDS
* I 8 D 8
MCW R1 MOVE NUM LSDS TO ACC MSDS (CHAIN)
* I 5 D 6
MCW ACC,R1
* I 8 D 14
* ROTATE R2 RIGHT BY FIVE CHARACTERS
MCW R2-5,ACC MOVE NUM MSDS TO ACC LSDS
* I 8 D 4
MCW R2 MOVE NUM LSDS ACC MSDS (CHAIN)
* I 5 D 10
MCW ACC,R2
* I 8 D 14
MCW R2,SUM
* I 8 D 14
A R1,SUM
* I 8 D 14
MZ @0@,SUM-6 IGNORE OVERFLOW
* I 8 D 2
MCW R2,R1
* I 8 D 14
MCW SUM,R2
* I 8 D 14
MRRTN B MRRTN RETURN TO CALLER
* I 5
|
Ronald Mak/SJSU
Robert Garner
I slightly modified your program, attached, to run under Python 3.2 (my MacBookPro?s default),
An e-mail from Ron Mak dated Nov 29, 2019
from Mike Albaugh, Nov 11, 2019 5:52pm
Did you get a chance to corner/ask Knuth last weekend if he knew of an efficient random number
generator for a decimal/character-oriented computer like our 1401?*
I?ve asked Ron Mak if he has any ideas.
Generate 1,000,000 random values and you?ll get a much nicer bell curve. How long will that take on the 1401?
Ron,
and to use the standard matplotlib histogram routine (not the prettier seaborn plotting library, which I need to learn. :)
Here?s the resulting histogram of your sum of 100 ?Mak Random? variables ? same as yours. :)
My plan is to try higher accumulated sums and then next run the Diehard random generator test suite. :))
This is fun exploring your efficient random number generator for 1400-class computers. :)
- Robert
Subject: Normally distributed random numbers on the 1401
From: Ronald Mak/SJSU
Date: Fri, Nov 29, 2019 2:09 pm
To: Robert Garner
Cc: Marc Verdiell
Hi, random fans.
I hope you all had a great Thanksgiving! Please enjoy some of my leftover turkey:
I hacked together a 1401 Autocoder program that generates, prints, and graphs 10,000 normally distributed random
numbers (i.e., they fit a bell curve). As in my previous program, I use my double-rotation algorithm to generate uniformly
distributed random numbers. In this program, I keep a running sum of the last 100 uniform random numbers. I accomplish
this by maintaining a circular buffer of the last 100 numbers. Each time I generate a new uniform random number, I
subtract the oldest number in the buffer from the sum, add the new number to the sum, and enter the new number
into the buffer to replace the oldest. According to the Central Limit Theorem of statistics, all the averages of the
individual sets of 100 buffered numbers will approach a normal distribution. I chose sample sizes of 100 for the
buffer because on the 1401, you can divide by 100 is by simply ignoring the last two digits of the sum.
I?ve attached the Autocoder program and the Python program for comparison. The outputs and graphs of both programs match,
so either I got them both right or they?re both wrong. To run the Python program in a terminal window:
ipython -i MakNormG.py
The ?G? is for ?graph?, which opens in a separate window.
Confused by all this? No, I?m not a statistician. I don?t even play one on TV. I only teach the subject ...
-- Ron
P.S. I noticed a problem with ROPE, which I believe some of you have encountered, and perhaps my former top student
Luca has fixed. If you accidentally send the 1401 simulator into an infinite loop, and you attempt to recover by
aborting ROPE, the simulator continues to run! ROPE forks the simulator as a separate Java thread, and normally,
it shuts down the thread when your 1401 program completes. But if you kill ROPE with an abort signal (control-C,
force kill, or whatever), you will have to kill the simulator process manually (e.g., kill -9 i1401r). Otherwise, the zombie
process holds onto its files, and when you restart ROPE, you will have problems accessing those files.
Ronald Mak
Attachments included:
http://www.cs.sjsu.edu/~mak/
Department of Computer Engineering
Department of Computer Science
Department of Applied Data Science
San Jos? State University
One Washington Square
San Jos?, CA USA 95192
?On two occasions I have been asked, ?Pray, Mr. Babbage, if you
put into the machine wrong figures, will the right answers come
out?? I am not able rightly to apprehend the kind of confusion of
ideas that could provoke such a question.?
-- Charles Babbage, 1791-1871
World?s first computer scientist
?The purpose of computing is insight, not numbers.?
-- Richard Hamming, 1915-1998, Mathematician
MakNormG.s,
MakNormG.lst,
MakNormG.out,
MakNormG.py,
Screen Shot 2019-11-29 at 2.08.31 PM.png
> Mike,
>
> Did you get a chance to corner/ask Knuth last weekend if he knew of an efficient random number
> generator for a decimal/character-oriented computer like our 1401?
Yes and no. I mentioned the project and that I had cracked open his book for some tips, but of course blew my credibility when I
mis-remembered which volume. He correctly said "Seminumerical Algorithms", which made sense, but of course my memory of taking
it off the shelf said "Fundamental Algorithms". When I got home I looked at the book itself sitting on my desk, and Surprise, Surprise he was right.
Anyway, I suspect that section on Linear Congruential in the _right_ book (that is, shelved to the right of the one I mis-remembered :-)
has plenty of tips, although it wouldn't be a textbook without having the student work exercises leading to enlightenment.
I see you have included Van, which is great, because I suspect the real slog-work is going to be the process of adding a RNDOM() subroutine
to the 1401 library, creating a new compiler tape that includes it. MY plan, such as it is, is to try to do _any_ subroutine and call it from FORTRAN.
Compared to that, the RNDOM subroutine itself is fairly simple. The one in the example code is a classic Linear Congruential, of the form
(expressed in C:
unsigned int seed;
unsigned int rndom() {
seed = ((seed * A) + C) % M);
return seed;
}
with some faffing around to convert the range from 0 to 65535 to the range 0.0 to 1.0-epsilon, for compatibility with the 7090 version.
For my original version, the constant M is 65536, because the original version was in fact written in C (and simultaneously 68000 assembly).
One of the few things C guarantees about arithmetic is that "unsigned int" will be evaluated as an actual two's complement number,
so M = 65536 can simply be a mask with 0xFFFF. IT is common with Linear Congruential PRNGs to pick an "easy" M like this. But of course
on a decimal machine, that is not an easy modulus.
A and C must be chosen (primarily having no prime factors in common with M) to avoid issues with sequence length.
Seminumerical Algorithms has a section that is a great start, along with the exercises.
But of course when attempting the choice of A and C (Given M) one should probably start with some way to evaluate the results.
Given the vast amount of memory and speed that modern computers need to properly render Cat Videos, they are well equipped to
actually do these tests relatively quickly, even for a nine-decimal digit (to contain the equivalent of the 7090's mantissa,
and then some.
So, I'd love to see someone come up with appropriate tests, either in general or "good enough" that after reducing to 0..11,
the number of occurrences of each value are reasonably equal, and that sequences (R1, R2, R3) from the output are also reasonably
equally distributed. Beware that human generated attempts at random numbers often fail this test, because they are light on
"can't happen" sequences (e.g. 1,2,3 or 7,7,7) that are just as likely as any of the other 1000 (or 1728 :-)
Note that my existing generator is a bit shy of 6 digits (there's a reason many computers had 18-bit integers until
the fetish for 8<
> *
>
> I?ve asked Ron Mak if he has any ideas.
> (As he had authored The Java Programmer?s Guide to Numerical Computing).
> Ron ?> Perhaps you might assign the question to one of your more engaged students. :)) Thanks!! :)))
Hey, I'd love so help, at least with testing, and if someone is ambitious enough to find some good A and C,
it could be fun.
Meanwhile, I need to get back to trying to understand the 1401 Fortran subroutine library/linking process.
BTW: anybody getting this only now, I swear my original html did not produce "Code Blue". No idea,
other than it has been quite some time since it was OK to feed code through a modern email agent
and try to compile and run it. (What we got back, didn't live too long")
> - Robert
>
> * This is your current random number generator (in 1401 FORTRAN).
> When it was running last week, it felt like it took about 4 seconds per invocation/monostich.
> 206 ISEED = (ISEED * 13849) + 23861
> C TAKE MODULO 65536 TO MIMIC ORIGINAL BINARY
> ITOP = ISEED/65536
> ISEED = ISEED - (ITOP * 65536)
> C CONVERT TO FLOAT AND MAP 0..65535. to 0..1.0
> RNDNO = ISEED
> RNDNO = RNDNO/65535.
Note that the slowness is almost certainly two divides, one floating point.
Using a "machine friendly" M would not help this, as Fortran of this era
did not have a shift operator (in keeping with the attempt to be radix-agnostic).
That's why any decimal version will have to be in assembly language to gain
much.
Thanks to all,
Mike
Mike,
(As he had authored The Java Programmer?s Guide to Numerical Computing).
Ron ?> Perhaps you might assign the question to one of your more engaged students. :)) Thanks!! :)))
Cheers,
- Robert
* This is your current random number generator (in 1401 FORTRAN).
When it was running last week, it felt like it took about 4 seconds per invocation/monostich.
206 ISEED = (ISEED * 13849) + 23861
C TAKE MODULO 65536 TO MIMIC ORIGINAL BINARY
ITOP = ISEED/65536
ISEED = ISEED - (ITOP * 65536)
C CONVERT TO FLOAT AND MAP 0..65535. to 0..1.0
RNDNO = ISEED
RNDNO = RNDNO/65535.